Im Grundlagenlabor kommt immer wieder die Frage auf, wie mittels Kleinsignalersatzschaltbild/Wechselstromersatzschaltbild die Formeln für die Wechselstromparameter wie Verstärkung, Eingangswiderstand, Ausgangswiderstand bestimmt werden können.
In Standardwerken wie Tietze Schenk wird dies als Trivial angesehen und nicht weiter darauf eingegangen. Aus diesem Grund möchte ich für eine einfache Basisschaltung das Vorgehen erläutern.
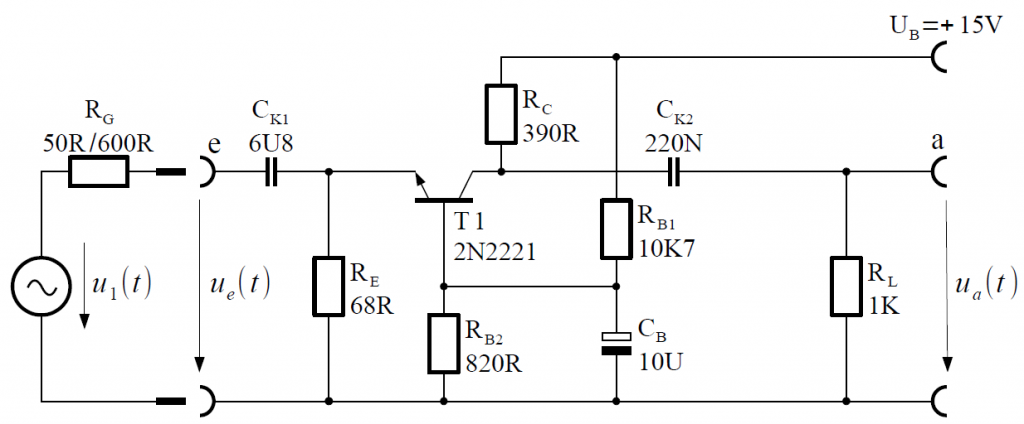
Ziel ist nun den dynamischen Ausgangswiderstand ohne RL zu bestimmen. Zunächst benötigen wir das Wechselstrom-Ersatzschaltbild der Schaltung. Dazu wird das Wechselstrom-Ersatzschaltbild des Transistors (Spannungsrückwirkung vernachlässigt) um die in der Schaltung enthaltenen Bauteile erweitert.
Hierzu gelten folgende Regeln:
- Nicht gesteuerte Spannungsquellen sind für Wechselspannung als Kurzschluss anzusehen
- Nicht gesteuerte Stromquellen sind für Wechselspannung als Leerlauf anzusehen
- Zusätzlich betrachten wir auch alle Kondensatoren als Kurzschluss für Wechselspannung. Somit entfallen RB1 und RB2. Später wird noch diskutiert, wie diese in das Modell zu integrieren sind.
Wir erhalten folgendes Ergebnis.
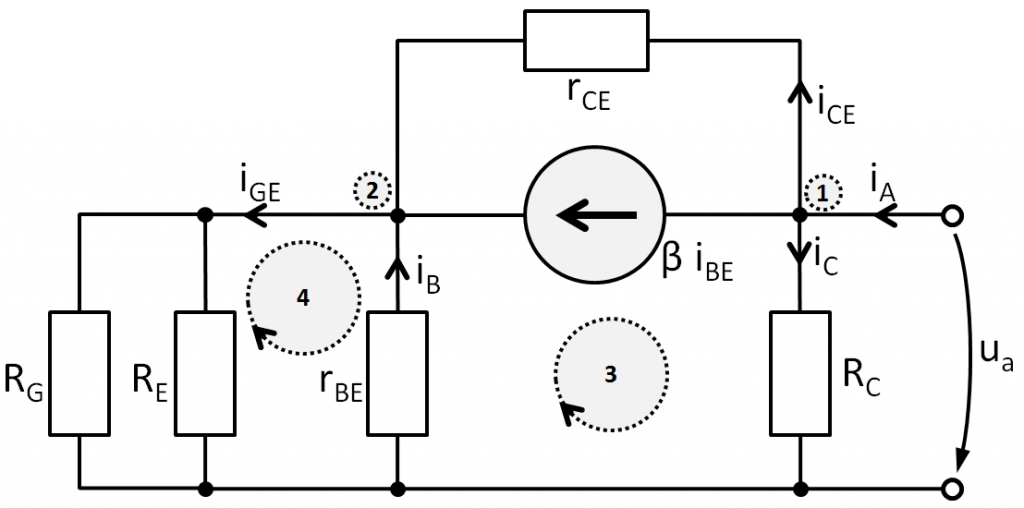 Mit den angegebenen Maschen und Knoten, ergeben sich folgende Gleichungen:
Mit den angegebenen Maschen und Knoten, ergeben sich folgende Gleichungen:
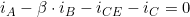
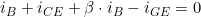
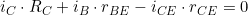
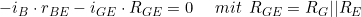
Bevor wir nun Anfangen, die Formeln umzustellen, sollte überlegt werden, was zu bestimmen ist. Wir wollen den Ausgangswiderstand in Abhängigkeit der Widerstände und β.
)
In den Formeln haben wir die Unbekannten 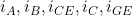 , wir benötigen aber
, wir benötigen aber 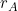 . Zunächst müssen wir einen Zusammenhang zu
. Zunächst müssen wir einen Zusammenhang zu 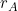 herstellen.
herstellen.
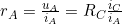
Somit müssen nur die Unbekannten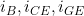 entfernt werden.
entfernt werden.
iGE eliminieren, da nur in 4 und 2 enthalten
4. nach iGE umstellen und in 2. einsetzen liefert
4. 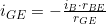
2. 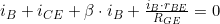
iB eliminieren
2. nach iB umstellen und in 1. und 3. einsetzen
2. )=-i_{CE}&space;\rightarrow&space;i_{B}=-\frac{i_{CE}}{1+\beta+\frac{r_{BE}}{R_{GE}}})
1. 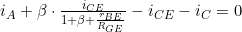
3. 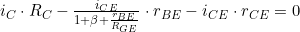
iCE eliminieren
3. iCE umstellen und in 1. einsetzen
3. 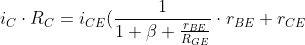\rightarrow&space;i_{CE}=\frac{i_{C}\cdot&space;R_{C}}{\frac{1}{1+\beta+\frac{r_{BE}}{R_{GE}}}\cdot&space;r_{BE}+r_{CE}}\rightarrow&space;i_{CE}=\frac{i_{C}\cdot&space;R_{C}\cdot(1+\beta+\frac{r_{BE}}{R_{GE}}))}{r_{BE}+r_{CE}\cdot(1+\beta+\frac{r_{BE}}{R_{GE}})})
1.}-\frac{i_{C}\cdot&space;R_{C}\cdot(1+\beta+\frac{r_{BE}}{R_{GE}}))}{r_{BE}+r_{CE}\cdot(1+\beta+\frac{r_{BE}}{R_{GE}})}-i_{C}=0\rightarrow&space;i_{A}-\frac{i_{C}\cdot&space;R_{C}\cdot(1+\frac{r_{BE}}{R_{GE}}))}{r_{BE}+r_{CE}\cdot(1+\beta+\frac{r_{BE}}{R_{GE}})}=i_{C})
rA bestimmen
}{r_{BE}+r_{CE}\cdot(1+\beta+\frac{r_{BE}}{R_{GE}})})\rightarrow&space;\frac{i_{C}}{i_{A}}=\frac{1}{1+\frac{R_{C}(1+\frac{r_{BE}}{R_{GE}})}{r_{BE}+r_{CE}(1+\beta+\frac{r_{BE}}{R_{GE}})}}\rightarrow&space;r_{A}=R_{C}\cdot\frac{i_{C}}{i_{A}}=\frac{R_{C}}{1+\frac{R_{C}(1+\frac{r_{BE}}{R_{GE}})}{r_{BE}+r_{CE}(1+\beta+\frac{r_{BE}}{R_{GE}})}}=\frac{1}{\frac{1}{R_{C}}+\frac{1+\frac{r_{BE}}{R_{GE}}}{r_{BE}+r_{CE}(1+\beta+\frac{r_{BE}}{R_{GE}})}})
Es ist eine Parallelschaltung zu erkennen. Zur Vereinfachung können wir ansetzen}{1+\frac{r_{BE}}{R_{GE}}})
Wir könnten an dieser Stelle abbrechen, nach Tietze Schenk wird noch rC als Fakor herausgezogen.
![\bg_white D=\frac{r_{BE}+r_{CE}(1+\beta+\frac{r_{BE}}{R_{GE}})}{1+\frac{r_{BE}}{R_{GE}}}=r_{CE}\cdot \frac{\frac{r_{BE}}{r_{CE}}+1+\beta +\frac{r_{BE}}{R_{GE}}}{1+\frac{r_{BE}}{R_{GE}}} \\D=r_{CE}\cdot (1+\frac{\frac{r_{BE}}{r_{CE}}+\beta }{1+\frac{r_{BE}}{R_{GE}}})=r_{CE}\cdot (1+\frac{R_{GE}}{r_{CE}}\cdot \frac{r_{BE}+\beta\cdot r_{CE} }{R_{GE}+r_{BE}})\rightarrow \\r_{A}=R_{C}||[r_{CE}\cdot (1+\frac{R_{GE}}{r_{CE}}\cdot \frac{r_{BE}+\beta\cdot r_{CE} }{R_{GE}+r_{BE}})]](http://latex.codecogs.com/gif.latex?\bg_white&space;D=\frac{r_{BE}+r_{CE}(1+\beta+\frac{r_{BE}}{R_{GE}})}{1+\frac{r_{BE}}{R_{GE}}}=r_{CE}\cdot&space;\frac{\frac{r_{BE}}{r_{CE}}+1+\beta&space;+\frac{r_{BE}}{R_{GE}}}{1+\frac{r_{BE}}{R_{GE}}}&space;\\D=r_{CE}\cdot&space;(1+\frac{\frac{r_{BE}}{r_{CE}}+\beta&space;}{1+\frac{r_{BE}}{R_{GE}}})=r_{CE}\cdot&space;(1+\frac{R_{GE}}{r_{CE}}\cdot&space;\frac{r_{BE}+\beta\cdot&space;r_{CE}&space;}{R_{GE}+r_{BE}})\rightarrow&space;\\r_{A}=R_{C}||[r_{CE}\cdot&space;(1+\frac{R_{GE}}{r_{CE}}\cdot&space;\frac{r_{BE}+\beta\cdot&space;r_{CE}&space;}{R_{GE}+r_{BE}})])
Maxima
Natürlich kann das erstellte Gleichungssystem auch mittels eines Computer Algebra System (CAS) gelöst werden. Als Beispiel habe ich die Berechnungen mittels Maxima realisiert. Hier das Skript Ausgangswiderstand Basisschaltung.
Ausblick
Zur Bestimmung anderer Kennwerte muss das Kleinsignalersatzschaltbild angepasst werden. So ist für die Spannungsverstärkung der Eingang wieder einzufügen und der Generatorwiderstand ist dazu in Reihe. Danach ist das Vorgehen zur Berechnung ähnlich.
Sind die Kondensatoren nicht zu vernachlässigen ist mit deren Blindwiderstand zu rechnen. Durch die imaginären Werte wird die Lösungen der Gleichungen sehr aufwändig, weshalb hier CAS eingesetzt werden sollten. Man erhält eine Lösung in Abhängigkeit der Frequenz, kann also die Verstärkung mit einer Zahl beschreiben sondern muss den Frequenzgang usw. angeben.